近日,数学学院黄寒松教授与美国范德堡大学郑德超教授在多重复变函数与算子代数交叉领域取得重要研究进展,其合作论文《Multiplication operators on the Bergman space of bounded domains》发表于数学领域知名期刊Advances in Mathematics(2025年第461卷)。该期刊为综合性数学权威刊物,致力于发表具有深刻理论价值与广泛影响力的原创成果。

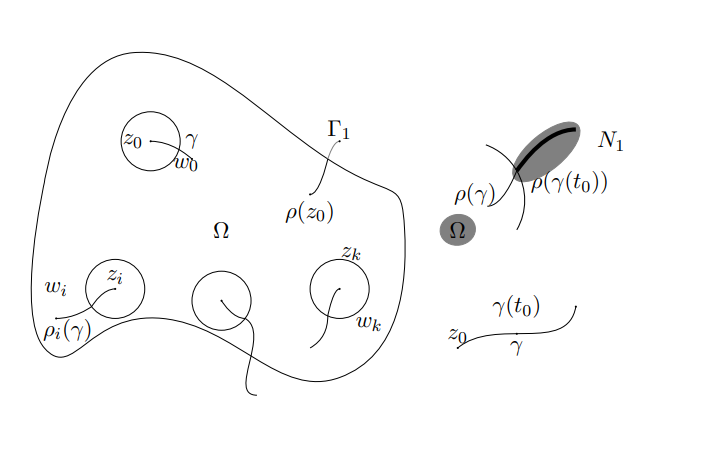
Bergman空间上乘法算子的代数结构研究是泛函分析与多复变函数论交叉领域的经典课题。该论文系统研究了高维有界域上全纯映射诱导的一组乘法算子及其生成von Neumann代数的精细结构。通过引入局部逆映射与L_a ^2-可移除性(L_a^2-removable)等创新工具,作者们建立了乘法算子相关的von Neumann代数维数和相关Riemann面的连通分支数相等。研究核心难点在于高维复几何的复杂性:相较于一维情形解析函数临界点集的离散性,高维临界集呈现为解析簇结构,需深入分析其与L_a^2可移除性间的本质关联。该成果体现了算子理论、复几何与函数论方法的深度融合。
自上世纪80年代以来,Ron Douglas、Mihai Putinar、Kehe Zhu等学者在一维情形对乘法算子的约化子空间理论做出奠基性工作,而高维情形仍存在大量未解问题。该研究针对该领域若干开放问题提出了新的分析思路,其方法或可为多复变算子代数的相关研究提供理论参考。


